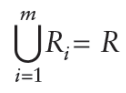- deduzir dependências funcionais a partir de um conjunto dado;
- junção sem perda e preservação de dependências funcionais;
- projeto relacional por síntese;
Fecho de DF – F+
Seja F o conjunto de dependências funcionais que são especificadas no esquema de relação R, o conjunto de todas as dependências que incluem F e todas as dependências que podem ser deduzidas de F, é chamado de fechamento de F, ou fecho de F, sendo denotado por F+.
Obs.: uma DF X → Y é deduzida de um conjunto de dependências F especificado em R, SE:
Sempre que r satisfizer todas as dependências em F, ENTÃO X → Y também se mantém em r.
Fecho de DF – F+ – Exemplo
F = {(Dep_nr → Cpf_gerente), (Cpf_gerente → Telefone_ger)}
F |= (Dep_ nr → Telefone_ger); % Lê-se: de F deduzimos…
Como não há mais DF a deduzir de F, temos que:
F+ = F ∪ {(Dep_ nr → Telefone_ger)}
Regras de inferência em DF
Fecho de X sob F – X+
X+ sob F – Exemplo
Equivalência de conjuntos de DF
Equivalência de conjuntos de DF –
Exemplo/Exercício calcule F+ e G+
Conjunto mínimo de DF
Cobertura mínima de F
Alg. 16.2 – Cobertura mínima de F
Alg. 16.2a – Chave
Decomposição de R
O conjunto F de dependências funcionais que devem ser mantidas nos atributos de R é especificado pelos projetistas de banco de dados e se torna disponível aos algoritmos de projeto.
Ao utilizar as dependências funcionais, os algoritmos decompõem o esquema de relação universal R em um conjunto de esquemas de relação D = {R1, R2, …, Rm}, que se tornará o esquema do banco de dados relacional; D é chamado de decomposição de R.
Preservação de atributo
D = {R1, R2, …, Rm}, temos de garantir que cada atributo em R aparecerá em pelo menos um esquema de relação Ri na decomposição, de modo que nenhum atributo seja perdido. Formalmente, temos
Esta é chamada de condição de preservação de atributo de uma decomposição.
Preservação de dependência – Intuição
Seria útil se cada dependência funcional X→Y especificada em F aparecesse diretamente em um dos esquemas de relação Ri na decomposição D ou pudesse ser deduzida das dependências que aparecem em alguma Ri.
Informalmente, essa é a condição de preservação de dependência
Preservação de dependência – Definição
Preservação de dependência e 3FN
Junção sem perda (não aditiva)
Alg. 16.3 – Testa junção não aditiva
Teste de junção não aditiva para
decomposições binárias
Decomposições sucessivas
Preservação de dependência e 3FN
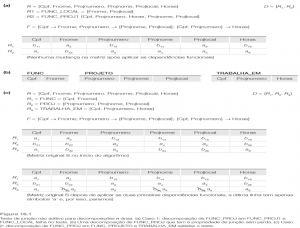
O Algoritmo 16.4, a seguir, cria uma decomposição de preservação de dependência D = {R1, R2, …, Rm} de uma relação universal R com base em um conjunto de dependências funcionais F, tal que cada Ri em D está na 3FN.
Isso garante apenas a propriedade de preservação de dependência; mas não garante a propriedade de junção não aditiva.
Alg. 16.4 – Síntese para 3FN com preservação de dependência