Motivação: alguns problemas de redundância não
são detectados pelas DF
Então, outras dependências são definidas, por
exemplo:
Dependências Multivaloradas
Dependências de Junção
Dependências de Inclusão
Dependência Multivalorada – O Problema
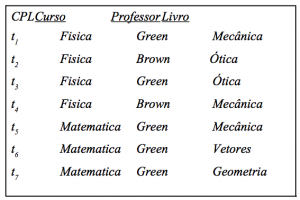
Seja a relação CPL(curso, professor, livro), onde:
– O professor P pode lecionar o curso C
– O livro L é recomendado para o curso C
Chave é CPL
Livros e professores são independentes
Está na FNBC, mas há redundância
Sugere outra FN que nos leve a normalização de CPL para CP e CL
Dependência Multivalorada – Intuição
Sejam r, R, X e Y conforme definido, a dependência multivalorada X → → Y é válida sobre r de R se para cada valor de X em r está associado um conjunto de valores de Y e esse conjunto é independente dos valores de Z=R – (X∪ Y)
• Intuitivamente o valor de um atributo determina um conjunto de valores de outro atributo!!!
Dependência Multivalorada – Definição
15: as tuplas t1, t2, t3 e t4, não são necessariamente distintas.
Dependência Multivalorada-Exemplo 1
Dependência Multivalorada–Exemplo 2
Dependência Multivalorada – Definição alternativa
Se X → → Y Então
πYZ(σX=x(R))=πY(σX=x(R)) x πZ(σX=x(R)).
Garante que dado o valor de X os valores de Y e Z são independentes.
Se existe ti com (X=A e Y=B) e existe tj com (X=A e Z=C) Então deve existir tk com (X=A, Y=B e Z=C).
Dependência Multivalorada – Propriedades
• toda dependência funcional é dependência multivalorada mas o recíproca não é necessariamente verdadeira
• Se (X→ → Y) e (Z=R-X ∪ Y) então X → → Z
• Se Y for subconjunto de X ou R=(X ∪ Y) então a MVD (X → → Y) é trivial
• Se a MVD não for trivial, para garantir a MVD, teremos que repetir valores em tuplas, gerando redundância…isto leva à 4FN
Quarta forma normal – 4FN
Dependência de Junção
Quinta forma normal – 5FN
Dependência de Junção – Exemplo
Exemplo: Seja X = (ecod, pno) e Y=(ecod, place)
e SKILL = X natural join Y
● DJ(X, Y) é uma dependência de junção em SKILL
● SKILL (ecod, pno, place) não está na 5FN pois X e Y não contêm uma superchave de SKILL
● Como vimos anteriormente, SKILL sequer está na 4FN. De fato a dependência multivalorada é um caso particular de dependência de junção, generalizando: DJ(X, Y) ≡ (X∩ Y) → → (X-Y)
Quinta forma normal – 5FN – Exemplo
Exemplo: está na 5FN
emp(ecod, ename, title)
proj(pno, pname, budget)
asg(ecod, pno, resp, dur)
pay(title, sal)
Obs: – uma relação na 5FN não pode ser decomposta sem perda de informação
– dependência de inclusão: define que algumas colunas estão contidas em outras. Chave estrangeira é um exemplo de dependência de inclusão
Normalização 2 – Considerações finais
A decomposição multivias para a 5FN é restrição semântica bastante peculiar e a normalização para a 5FN raramente é feita nestes termosUma alternativa à decomposição da relação universal é utilizar ferramentas de projeto conceitual e mapeamento para o relacional.
Por exemplo, um mapeamento do Modelo de Entidades e Relacionamentos para o Modelo Relacional gera esquemas de BD na terceira forma normal.