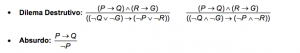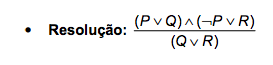| Identificação | Formula H | Fórmula G | ||||
| Dupla Negativa | ¬(¬E) | E | ||||
| Propriedades de Identidade |
|
|
||||
| Propriedades Complementares |
|
|
||||
| Leis de DeMorgan |
|
|
||||
| Contraposição | E → R | ¬R → ¬E | ||||
| Propriedades de Substituição |
|
|
||||
| Propriedades Comutativas |
|
|
||||
| Propriedades Associativas |
|
|
||||
| Propriedades Distributivas |
|
|
||||
| Prova Condicional | E → (R → S) | (E ∧ R) → S |
Exercício: Sejam P e Q ∈ L∅. Demonstre, com o auxílio das equivalências clássicas, que as fórmulas abaixo são equivalentes: E = Q → (Q ∧ P) e G = (¬Q ∨ Q) ∧ (¬Q ∨ P).
Solução: Q → (Q ∧ P)
⇔ ¬Q ∨ (Q ∧ P) (aplicando a Propriedade de Substituição do →)
⇔ (¬Q ∨ Q) ∧ (¬Q ∨ P) (aplicando a Propriedade Distributiva)
Métodos de Validação de Fórmulas
- Tabela-Verdade
A tabela-verdade é um método de validação baseada na força bruta. Isso ocorre, porque devemos mapear todas as possíveis combinações dos símbolos/variáveis proposicionais.
Assim, seja P uma fórmula proposicional e α o conjunto de variáveis proposicionais existentes em P (α = {X1, X2, …, XN}). A tabela-verdade de P é uma tabela com pelo menos N+1 colunas e exatamente 2N linhas. As N primeiras colunas representam as variáveis proposicionais, enquanto a (N+1)-ésima coluna representa a fórmula P. Cada linha representa uma possível combinação de valores (T ou F) das variáveis pertencentes a α e o valor verdade de P resultante desta combinação.
TABELA-VERDADE X PROPRIEDADES SEMÂNTICAS
1- Uma fórmula é uma tautologia se a última coluna de sua tabela-verdade contém somente
valores T ou 1.
2- Uma fórmula é uma contradição se a última coluna de sua tabela-verdade contém somente
valores F ou 0 (zero).
3- Uma fórmula é factível se a última coluna de sua tabela-verdade contém pelo menos um valor
T ou 1.
4- Duas fórmulas são equivalentes semanticamente quando, para cada linha da tabela-verdade,
suas colunas apresentam o mesmo valor.
5- Uma fórmula G implica semanticamente na fórmula H se, para toda linha cujo valor da coluna
de G é verdadeiro, o valor da coluna de H também é verdadeiro.
- Árvore Semântica
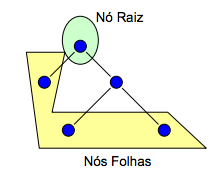
Este método determina a validade de uma fórmula a partir de uma estrutura denominada árvore.
Uma árvore é um conjunto de nós (vértices) ligados por arestas. Os nós finais são chamados “folhas”, o nó inicial é denominado “raiz”, enquanto os demais nós são intermediários.
Exemplo de Árvore:
Durante a validação, as arestas que ligam o nó raiz aos outros nós recebem um rótulo, indicando os possíveis valores de uma determinada variável proposicional, escolhida aleatoriamente. Se a partir de uma interpretação for possível obter o valor da fórmula, este é associado ao nó folha correspondente. Caso não seja possível tal aferição, cria-se mais duas arestas, aumentando a ramificação da árvore. Para a rotulação dessas arestas, escolhemos uma outra variável proposicional. Este processo é repetido até que todos os nós folhas tenham valores associados à fórmula.
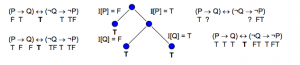
Exercício: Demonstre, através de árvores semânticas, a validade de H = (P → Q) ↔ (¬Q ∧ ¬P).
Solução:
ÁRVORE SEMÂNTICA X PROPRIEDADES SEMÂNTICAS
1- Uma fórmula é uma tautologia se só têm valores T ou 1 em seus nós folhas.
2- Uma fórmula é uma contradição se só têm valores F ou 0 (zero) em seus nós folhas.
3- Uma fórmula é factível se pelo menos um nó folha com valor T ou 1.
4- Duas fórmulas G e H são equivalentes semanticamente, se a árvore semântica
correspondente à fórmula G ↔ H for uma tautologia.
5- Uma fórmula G implica semanticamente na fórmula H, se a árvore semântica correspondente
à fórmula G → H for uma tautologia.
- Método da Negação ou Absurdo
O método da negação ou absurdo é um método geral de demonstração. Ele consiste em negar a afirmação que se deseja provar e, a partir de um conjunto de deduções, concluir um fato contraditório ou absurdo (ex: I[P] = T e I[P] = F).
A aplicação deste método é recomendada nos casos onde a negação da afirmação nos leva a casos determinísticos, ou seja, com uma única possibilidade de interpretação para a fórmula, pois isto simplifica a demonstração. Tal situação ocorre quando a negação acarreta a falsidade dos conectivos → e ∨ e a veracidade do conectivo ∧.
Exercício: Demonstrar, através do método da negação, a validade da Lei de Transitividade do
conectivo →: H = ((P → Q) ∧ (Q → R)) → (P → R)
Solução: validade = tautologia. Logo, devemos provar que ∀ I | I[H] = T.
Supondo que H NÃO é tautologia, então ∃ I | I[H] = F.
I[((P → Q) ∧ (Q → R)) → (P → R)] = F ⇒ I[((P → Q) ∧ (Q → R))] = T e I[(P → R)] = F
Para I[(P → R)] = F ⇒ I[P] = T e I[R] = F
Para I[((P → Q) ∧ (Q → R))] = T ⇒ I[P → Q] = T e I[Q → R] = T
Se I[P → Q] = T ⇒ I[P] = F e/ou I[Q] = T, mas como I[P] = T, logo: I[Q] = T
Se I[Q → R] = T ⇒ I[Q] = F e/ou I[R] = T, mas como I[R] = F, logo: I[Q] = F
ABSURDO: Q NÃO pode assumir dois valores (T e F) no mesmo instante.
Portanto, a suposição inicial está errada e H é tautologia.
O objetivo deste método é deduzir uma contradição / absurdo a partir da negação da fórmula em prova. Entretanto, nem sempre isto ocorre. Nestes casos, NADA se pode concluir sobre a veracidade da asserção inicial. Além disso, quando existem mais de uma possibilidade testada, originada de cláusulas e/ou, todas devem gerar uma contradição.
MÉTODO DA NEGAÇÃO OU ABSURDO X PROPRIEDADES SEMÂNTICAS
1- Uma fórmula H é uma tautologia se a suposição ∃ I | I[H] = F gerar contradição.
2- Uma fórmula H é uma contradição se a suposição ∃ I | I[H] = T gerar contradição.
3- Uma fórmula H é factível quando ela não for tautologia, nem contradição. Neste caso, basta
apresentar duas interpretações para H (I e J), onde I[H] = T e J[H] = F.
4- Duas fórmulas G e H são equivalentes semanticamente, se for possível provar que a fórmula
G ↔ H for uma tautologia.
5- Uma fórmula G implica semanticamente na fórmula H, se for possível provar que a fórmula
G → H for uma tautologia.
- Princípio da Indução Finita
Apesar de não fazer parte da lógica, este princípio é um dos principais métodos utilizados na demonstração de resultados. Na ciência da computação, tal princípio é usado para demonstrar resultados em linguagens formais, teoria de algoritmos, teoria dos códigos, etc.
Paradigma da Indução
Considere um conjunto de peças de dominó enfileiradas e enumeradas. Elas estão dispostas de modo que, se o dominó 1 é derrubado para direita, então o subseqüente (dominó 2) também cai, e assim sucessivamente.
Diante disto, surge a pergunta: “O que é suficiente para um dominó N cair?”
Resposta: que qualquer um dos dominós que o antecede caia para direita, ou seja, existem (N-1) condições suficientes.
Suponhamos que o dominó 1 caia para direita, logo o dominó N também cai. Agora surge outra pergunta: “Qual é a condição necessária para que o dominó 1 possa cair para direita?”.
Resposta: que os dominós subseqüentes possam ser derrubados.
A partir deste cenário, observamos que existem várias condições suficientes para que todos os dominós sejam derrubados. Exemplo:
Se o dominó 1 é derrubado para direita, então o dominó N cai, ou simplesmente, D1 → DN.
Dentre eles, destacamos 2 conjuntos:
1º conjunto:
• Condição básica: O dominó 1 é derrubado para direita.
• Condição indutiva: Seja N um nº arbitrário. Se o dominó N é derrubado para direita, então o dominó N+1 também cai.
2º conjunto:
• Condição básica: O dominó 1 é derrubado para direita.
• Condição indutiva: Seja N um nº arbitrário. Se todos os dominós até N são derrubados para direita, então o dominó N+1 também cai.
Note, que ambos tem a mesma condição básica. Entretanto, a condição indutiva é ligeiramente modificada.
O princípio da indução finita possui 2 formas que correspondem a estes conjuntos. Neste curso iremos abordar apenas a 1ª forma.
- 1a Forma de Indução
Suponha que para cada N (N ≥ 1), seja dada a asserção A(N). Para concluirmos que A(N) é verdadeira para todo inteiro N, deve ser possível demonstrar as seguintes propriedades:
• Base da Indução: A asserção A(1) é verdadeira.
• Passo Indutivo: Dado um inteiro N (N ≥ 1), se A(N) é verdadeira, então A(N+1) também é verdadeira.
Exercício: Demonstre, através do princípio da indução finita, que: dada a progressão geométrica ai+1 = ai+q, para q ≠ 1. A soma dos N primeiros termos desta progressão pode ser calculada por:
Formas Normais
As fórmulas da lógica proposicional podem ser expressas utilizando vários conjuntos de conectivos completos. Além disso, também podemos representá-las através de estruturas pré-definidas, denominadas formas normais. São elas:
• Forma Normal Disjuntiva (FND): se a fórmula é uma disjunção de conjunções de literais
(símbolos proposicionais ou suas negações).
• Forma Normal Conjuntiva (FNC): se a fórmula é uma conjunção de disjunções de literais.
Ex: H = (¬P ∧ Q) ∨ (¬R ∧ ¬Q ∧ P) ∨ (P ∧ S) FND
G = (¬P ∨ Q) ∧ (¬R ∨ ¬Q ∨ P) ∧ (P ∨ S) FNC
Obtenção das Formas Normais
Considere a fórmula: H = (P → Q) ∧ R. Podemos escrever H1 e H2, de modo que H1 seja H na FND e H2 seja H na FNC, com segue:
| P | Q | R | H |
| F | F | F | F |
| F | F | T | T |
| F | T | F | F |
| F | T | T | T |
| T | F | F | F |
| t | F | T | F |
| T | T | F | F |
| T | T | T | T |
2º Passo: Geração de H1 (FND).
– Extrair as linhas da tabela-verdade onde I[H] = T. Para cada linha N, gerar uma fórmula YN, formada apenas pela conjunção de literais, de modo que I[YN] = T, como apresentado abaixo:
2ª linha: I[P] = F, I[Q] = F, I[R] = T ⇒ Y2 = (¬P ∧ ¬Q ∧ R).
4ª linha: I[P] = F, I[Q] = T, I[R] = T ⇒ Y2 = (¬P ∧ Q ∧ R).
8ª linha: I[P] = T, I[Q] = T, I[R] = T ⇒ Y2 = (P ∧ Q ∧ R).
– Gerar H1 a partir da disjunção das fórmulas geradas no item anterior.
H1 = (¬P ∧ ¬Q ∧ R) ∨ (¬P ∧ Q ∧ R) ∨ (P ∧ Q ∧ R)
3º Passo: Geração de H2 (FNC).
– Extrair as linhas da tabela-verdade onde I[H] = F. Para cada linha N, gerar uma fórmula XN, formada apenas pela disjunção de literais, de modo que I[XN] = T, como apresentado abaixo:
1ª linha: I[P] = F, I[Q] = F, I[R] = F ⇒ X1 = (P ∨ Q ∨ R).
3ª linha: I[P] = F, I[Q] = T, I[R] = F ⇒ X3 = (P ∨ ¬Q ∨ R).
5ª linha: I[P] = T, I[Q] = F, I[R] = F ⇒ X5 = (¬P ∨ Q ∨ R).
6ª linha: I[P] = T, I[Q] = F, I[R] = T ⇒ X6 = (¬P ∨ Q ∨ ¬R).
7ª linha: I[P] = T, I[Q] = T, I[R] = F ⇒ X7 = (¬P ∨ ¬Q ∨ R).
– Gerar H2 a partir da conjunção das fórmulas geradas no item anterior.
H2 = (P ∨ Q ∨ R) ∧ (P ∨ ¬Q ∨ R) ∧ (¬P ∨ Q ∨ R) ∧ (¬P ∨ Q ∨ ¬R) ∧ (¬P ∨ ¬Q ∨ R)
Dedução de Teoremas
O processo de prova por dedução consiste em demonstrar que, dadas algumas expressões como verdadeiras (hipóteses ou premissas), uma nova sentença também é verdadeira. Quando isso ocorre, dizemos que a sentença provada é um teorema com respeito às hipóteses.
A prova de um teorema consiste em derivar a expressão desejada H a partir das hipóteses β, utilizando os recursos disponíveis em algum dos sistemas de dedução válidos (β |– H).
Definição (sistemas de dedução): também denominados sistemas formais, são completos (se β ⇒ H, então β |– H) e corretos (se β |– H, então β ⇒ H) e estabelecem estruturas que permitem a representação e dedução do conhecimento.
- TIPOS DE SISTEMAS DE DEDUÇÃO
Os sistemas de dedução podem ser divididos em 2 grupos, como segue:
• Sistemas de difícil implementação computacional:
Sistema Axiomático
Dedução Natural
• Sistemas mais adequados para implementação computacional:
o Tableaux Semânticos
o Resolução
Neste curso, apresentaremos o sistema axiomático e a resolução.
Sistema Axiomático
O sistema axiomático é uma estrutura para representação e dedução do conhecimento baseado em axiomas. Ele é definido pela composição de 4 elementos:
• Alfabeto da lógica proposicional;
• Conjunto de fórmulas proposicionais (Hipóteses)
• Subconjunto de fórmulas, denominados axiomas; e
• Conjunto de regras de inferência.
HIPÓTESES
As hipóteses ou premissas são fórmulas proposicionais tidas (assumidas) como verdadeiras.
Assim, caso se descubra que uma das hipóteses pode ser falsa, toda prova feita a partir desta hipótese perde sua validade.
AXIOMAS
Os axiomas representam o conhecimento dado a priori. No caso do sistema axiomático, este conhecimento é representado por tautologias.
O conjunto de fórmulas axiomáticas pode variar entre os sistemas axiomáticos. Porém, independente do conjunto adotado, o mesmo deve assegurar o sistema axiomático seja completo e correto.
Neste curso, adotaremos um sistema cujos axiomas são determinados pelos esquemas:
• Ax1 = ¬(H ∨ H) ∨ H ⇔ (H ∨ H) → H
• Ax2 = ¬H ∨ (G ∨ H) ⇔ H → (G ∨ H)
• Ax3 = (¬(¬H ∨ G)) ∨ ((¬(E ∨ H)) ∨ (G ∨ E)) ⇔ (H → G) → ((E ∨ H) → (G ∨ E))
sendo, H, G e E quaisquer fórmulas preposicionais.
REGRAS DE INFERÊNCIA
As regras de inferência são implicações semânticas. Elas são utilizadas para fazer inferências, ou seja, executar os “passos” de uma demonstração ou dedução.
Assim como os axiomas, o conjunto de regras de inferência adotado em um sistema axiomático pode variar, desde que mantenham as propriedades de completude e correção. Quanto menor o conjunto de regras de inferência, mais elegante é o sistema axiomático.
Abaixo serão listadas algumas regras de inferência que podem ser utilizadas em um sistema
axiomático:
OBS: A maioria dos sistemas axiomáticos costuma utilizar apenas o Modus Ponens (MP) como regra de inferência.
PROVA EM UM SISTEMA AXIOMÁTICO
Uma prova ou demonstração através do sistema axiomático consiste em apresentar a seqüência de passos necessários para derivar a fórmula desejada a partir das hipóteses. Cada passo pode ser a geração de um axioma ou a aplicação de uma regra de inferência.
Proposição: dado um teorema com as hipóteses H1, H2, …, HN e a fórmula a ser provada C. Ele é verdadeiro sempre que:
Exercício 1: Prove P → (S ∨ G) através de um sistema axiomático que utiliza todas as regras de
inferência apresentadas acima e com o seguinte conjunto de hipóteses:
P → (Q ∨ R)
Q → S
R → G
Solução:
– considerando as hipóteses:
P → (Q ∨ R) (1)
Q → S (2)
R → G (3)
– Aplicando o dilema construtivo entre (2) e (3), temos:
(Q ∨ R) → (S ∨ G) (4)
– Aplicando o silogismo hipotético entre (1) e (4), temos:
P → (S ∨ G) c.q.d
PROVA POR ABSURDO
Neste tipo de prova, nega-se a fórmula que se deseja provar, a inclui no conjunto de hipóteses e aplica as regras de inferência até se obter um absurdo.
Exercício: A partir das hipóteses abaixo e utilizando apenas o Modus Ponens (MP) como regra de inferência, prove P.
¬S → P
R ∨ ¬P
¬S
Solução:
– Considerando as hipóteses:
¬S → P (1)
R ∨ ¬P (2)
¬S (3)
¬P (4) Negação do teorema
– Aplicando a equivalência (G → H ⇔ ¬H → ¬G) em (1), temos:
¬P → S (5)
– Aplicando MP entre (4) e (5), temos:
S (6)
Como (6) contradiz (3), conclui-se que a suposição inicial (¬P) é falsa. Logo β |– P c.q.d.
DERIVAÇÃO SEM HIPÓTESES
Além das provas onde uma fórmula G é derivada a partir de um conjunto de hipóteses β (β |– G), existem casos onde o sistema axiomático não possui hipóteses (β é vazio) e a fórmula desejada é derivada somente a partir dos axiomas, denotamos: |– G.
Ex: Utilizando um sistema axiomático sem hipóteses e apenas com Modus Ponens como regra de inferência, prove (P ∨ ¬P).
– Para gerar uma sentença que contenha a fórmula a ser derivada, utilizamos o Ax3 com H = (P ∨ P), E = ¬P e G = P, temos:
((P ∨ P) → P) → ((¬P ∨ (P ∨ P)) → (P ∨ ¬P)) (1)
– Note que a parte antecedente de (1) pode ser gerada a partir de Ax1 para H = P:
(P ∨ P) → P (2)
– Aplicando MP entre (2) e (1), temos:
((¬P ∨ (P ∨ P)) → (P ∨ ¬P)) (3)
– A parte antecedente de (3) pode ser gerada a partir de Ax2 para H = P e G = P:
¬P ∨ (P ∨ P) (4)
– Aplicando MP entre (4) e (3), temos:
(P ∨ ¬P) c.q.d.
Resolução
Ao contrário do sistema axiomático, no método de resolução não se tem axiomas. Portanto, este método é definido pela composição dos seguintes elementos:
• Alfabeto da lógica proposicional;
• Conjunto de cláusulas, geradas a partir de fórmulas proposicionais (Hipóteses)
• Regra de inferência.
A resolução é um método de prova aplicado sobre fórmulas que estão na forma de conjunções de disjunções, conhecida como forma normal conjuntiva (FNC).
Ex: H = (P ∨ ¬Q ∨ R) ∧ (R ∨ Q) ∧ (¬P ∨ ¬R ∨ ¬P)
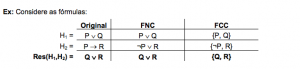
Cada fórmula é, então, representada na forma de conjunto de cláusulas (FCC). Nesta notação, cada disjunção é um subconjunto (cláusula), onde o conectivo ou é trocado por uma vírgula. Além disso, as vírgulas entre os subconjuntos representam a conjunção (conectivo e) das disjunções.
Ex: H = {{P, ¬Q, R}, {R, Q}, {¬P, ¬R}}
Note que no exemplo acima, {¬P, ¬R} representa (¬P ∨ ¬R ∨ ¬P). Isto ocorre, pois não se representa duplicidade na notação de conjuntos (FCC).
REGRA DE INFERÊNCIA
O mecanismo de inferência da resolução utiliza apenas uma regra, denominada regra de resolução, como segue: